Test for conditional quantile change in GARCH models

Abstract

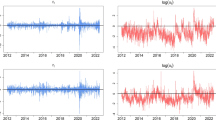
In this study, we consider the problem of detecting a change point in the conditional quantile of GARCH models. The task is essential in risk management as the conditional quantile is utilized to calculate the value-at-risk (VaR) of asset prices. We propose the cumulative sum (CUSUM) tests based on the residuals and derive their limiting distributions under mild conditions. We also demonstrate the validity of the tests by conducting Monte Carlo simulations, followed by a real data analysis of the exchange rate between the US Dollar and Korean Won and the Korea composite stock price index.

Appendix

We here provide a proof of Theorem 2.1 in Sect. 2. All necessary notations are introduced in Sect. 2.

Proof of Theorem 2.1

We first handle ${\hat{T}}_{n,1}$. Note that

$$\begin{aligned}&\frac{1}{\sqrt{n}}\max _{1\le k\le n}\left| \sum _{t=1}^k y_{t-1}^2\{ \psi _\tau (y_t-{\hat{q}}_t (\tau ))- \psi _\tau (y_t-q_t^0 (\tau ))\}\right. \\ &\qquad \left. -\frac{k}{n}\sum _{t=1}^n y_{t-1}^2\{\psi _\tau (y_t-{\hat{q}}_t (\tau ))- \psi _\tau (y_t-q_t^0 (\tau ))\}\right| \\ &\quad \le \frac{2}{\sqrt{n}}\max _{1\le k\le n}\left| \sum _{t=1}^k y_{t-1}^2\{ I(\epsilon _t \le {\hat{\xi }}{\hat{\sigma }}_t/\sigma _{t0}) -F({\hat{\xi }}{\hat{\sigma }}_t/\sigma _{t0} )+F(\xi _0 )-I(\epsilon _t \le \xi _0)\}\right| \\ &\qquad +\frac{1}{\sqrt{n}}\max _{1\le k\le n}\left| \sum _{t=1}^k y_{t-1}^2 ( F({\hat{\xi }}{\hat{\sigma }}_t/\sigma _{t0} )-F(\xi _0 ))\right. \\ &\qquad \left. -\frac{k}{n}\sum _{t=1}^n y_{t-1}^2 ( F({\hat{\xi }}{\hat{\sigma }}_t/\sigma _{t0} )-F(\xi _0 ))\right| {:}{=}A_n +B_n. \end{aligned}$$

Properly modifying the arguments used for analysing the asymptotic behavior of the sequential residual empirical process for ARMA and GARCH models (Bai, 1993; Koul, 2002; Lee & Kim, 2017; Lee et al., 1999), one can verify that $A_n =o_P (1)$. Below we provide a condensed proof without going into great detail.

We put $g_t (\vartheta ) {:}{=}\xi {\tilde{\sigma }}_t (\theta )/\sigma _{t0}-\xi _0$ and

$$\begin{aligned} I_k{:}{=} \frac{1}{\sqrt{n}}\sum _{t=1}^{k}y_{t-1}^2\Big \{I({\epsilon }_{t}\le \xi _0+g_t ({\hat{\vartheta }}))-F(\xi _0+g_t ({\hat{\vartheta }}))-F(\xi _0)+I(\epsilon _t\le \xi _0)\Big \}. \end{aligned}$$

For any $\delta \in (0,1)$, there exists $L>0$ such that $P(\hat{\vartheta }_{n}\in {\mathcal{N}}_{L/\sqrt{n}})\ge 1-\delta$, where ${\mathcal{N}}_{L/\sqrt{n}}$ is a compact neighborhood of $\vartheta _{0}$ with $\|\vartheta -\vartheta _{0}\|\le L/\sqrt{n}$ for all $\vartheta \in {\mathcal{N}}_{L/\sqrt{n}}$. For a positive real number $\eta$, we partition ${\mathcal{N}}_{L/\sqrt{n}}$ into a finite number, say, $N{:}{=}N(\eta )$ of subsets $D_1,\ldots ,D_N$ with diameter less than $\frac{\eta }{\sqrt{n}}$. We choose any points $\vartheta _j$ in $D_j$. Then, when ${\hat{\vartheta }}_n \in D_j$, we have

$$\begin{aligned} I({\epsilon }_{t}\le \xi _0+ g_t (\vartheta _j )+g_{tj}^{-})\le I({\epsilon }_{t}\le \xi _0+g_{t} ({\hat{\vartheta }}))\le I({\epsilon }_{t}\le \xi _0+g_t (\vartheta _j)+g_{tj}^+ (\vartheta )) \end{aligned}$$

with $g_{tj}^{-}=\inf _{\vartheta \in D_j} g_t (\vartheta )-g_t (\vartheta _j)$ and $g_{tj}^{+}=\sup _{\vartheta \in D_j} g_t (\vartheta )-g_t (\vartheta _j )$. Put

$$\begin{aligned} I_{kj}^+= & {} \frac{1}{\sqrt{n}}\sum _{t=1}^{k}y_{t-1}^2\Big \{I({\epsilon }_{t}\le \xi _0+g_t (\vartheta _j)+g_{tj}^+)-F(\xi _0+g_t (\vartheta _j)+g_{tj}^+)\\&-F(\xi _0)+I(\epsilon _t\le \xi _0)\Big \},\\ I_{kj}^-= & {} \frac{1}{\sqrt{n}}\sum _{t=1}^{k}y_{t-1}^2\Big \{I({\epsilon }_{t}\le \xi _0+g_t (\vartheta _j)+g_{tj}^-)-F(\xi _0+g_t (\vartheta _j)+g_{tj}^-)\\&-F(\xi _0)+I(\epsilon _t\le \xi _0)\Big \}. \end{aligned}$$

Then,

$$\begin{aligned} \max _{1\le k\le n} |I_k|\le \max _{1\le j\le N} \max _{1\le k\le n} |I_{kj}^+|+\max _{1\le j\le N} \max _{1\le k\le n} |I_{kj}^-|+R_n \end{aligned}$$

(8)

with

$$\begin{aligned} R_n= & {} \frac{1}{\sqrt{n}}\sum _{t=1}^{n}\max _{1\le j\le N} y_{t-1}^2 \sup _{\vartheta \in D_j}|F(\xi _0+g_t (\vartheta _j)+g_{tj}^+)-F(\xi _0+ g_t (\vartheta ))|\nonumber \\ &+\frac{1}{\sqrt{n}}\sum _{t=1}^{n}\max _{1\le j\le N} y_{t-1}^2\sup _{\vartheta \in D_j}| F(\xi _0+g_t (\vartheta _j)+g_{tj}^-)-F(\xi _0+ g_t (\vartheta ))|\nonumber \\ = & {} \eta O_P (1). \end{aligned}$$

(9)

Put

$$\begin{aligned} e_{tj}^+= & {} y_{t-1}^2\Big \{I({\epsilon }_{t}\le \xi _0+g_t (\vartheta _j)+g_{tj}^+)-F(\xi _0+g_t (\vartheta _j)+g_{tj}^+)-F(\xi _0)+I(\epsilon _t\le \xi _0)\Big \},\\ e_{tj}^-= & {} y_{t-1}^2\Big \{I({\epsilon }_{t}\le \xi _0+g_t (\vartheta _j)+g_{tj}^-)-F(\xi _0+g_t (\vartheta _j)+g_{tj}^-)-F(\xi _0)+I(\epsilon _t\le \xi _0)\Big \}, \end{aligned}$$

and $S_{kj}^+=\sum _{t=1}^{k}e_{tj}^+$ and $S_{kj}^-=\sum _{t=1}^{k}e_{tj}^-$ . Note that $\{(S_{kj}^+, {\mathcal{F}}_t); k=1,\ldots , n\}$, where ${\mathcal{F}}_t=\sigma (\epsilon _t, \epsilon _{t-1},\ldots )$, forms an array of martingales. Then, for any $\lambda >0$, using the sub-martingale inequality, we get

$$\begin{aligned}&P\Big (\max _{1\le j\le N}\max _{1\le k\le n} |I_{kj}^+|\ge \lambda \Big )\le P\Big (\max _{1\le j\le N}\frac{1}{\sqrt{n}}\max _{1\le k\le n} |S_{kj}^+|\ge \lambda \Big )\nonumber \\&\quad \le \sum _{j=1}^N P\Big (\max _{1\le k\le n}|S_{kj}^+|\ge \sqrt{n}\lambda \Big )\le \sum _{j=1}^N E S_{nj}^{+2p}/n^{p}\lambda ^{2p}. \end{aligned}$$

(10)

Furthermore, applying Rosenthal’s inequality (Hall & Heyde, 2014), we get

$$\begin{aligned} ES_{nj}^{+2p}\le C\left( E\left[ \sum _{t=1}^{n}E(e_{tj}^{+2}|{\mathcal{F}}_{t-1})\right] ^{p}+\sum _{t=1}^{n}E(e_{tn}^{+2p})\right) , \end{aligned}$$

(11)

for some $C>0$. Using the mean value theorem and the fact that $E\{y_{t-1}^4 |g_t (\vartheta _j)+g_{tj}^+|\}^{p} <\infty$, we can see that $E\Big [\sum _{t=1}^{n}E(e_{tj}^{+2}|{\mathcal{F}}_{t-1})\Big ]^{p}=O (n^{p/2})$, so that since $\sum _{t=1}^{n}E(e_{tj}^{+2p})= O(n)$, we have $ES_{nj}^{+2p}=O(n^{p/2}+n )$ uniformly in j by (11). This together with (10) implies $\max _{1\le j\le N}\max _{1\le k\le n} |I_{kj}^+|=o_P (1)$. Similarly, we can check that $ES_{nj}^{-2p}=O(n^{p/2}+n )$ uniformly in j, so that

$$\begin{aligned} \max _{1\le j\le N}\max _{1\le k\le n} |I_{kj}^-|=o_P (1). \end{aligned}$$

Combining this, (8) and (9) with an arbitrarily small $\eta$, we obtain $A_n= o_P (1)$. Meanwhile, using Taylor’s theorem up to order 2 and the ergodicity of $\{y_t\}$, one can easily verify that $B_n =o_P (1)$. This with ${\hat{\tau }}_{1}^2=\tau _1^2+o_P (1)$ indicates that ${\hat{T}}_{n,1}- T_{n,1}=o_P (1)$, and thus, ${\hat{T}}_{n,1}$ weakly converges to $\sup _{0\le s\le 1} | B^\circ (s)|$ due to (4).

Next, we deal with ${\hat{T}}_{n,2}$. Under the conditions of the Theorem 2.1, we first verify that (5) holds. Note that

$$\begin{aligned}&\max _{1\le k\le n}\left| \frac{1}{\sqrt{n}} \left| \sum _{t=1}^{k} {\hat{\delta }}_t^2 - \frac{k}{n}\sum _{t=1}^{n} {\hat{\delta }}_t^2 \right| - \frac{1}{\sqrt{n}} \left| \sum _{t=1}^{k} {\hat{\epsilon }}_t^2 - \frac{k}{n}\sum _{t=1}^{n} {\hat{\epsilon }}_t^2 \right| \right| \\ &\quad \le \frac{1}{\sqrt{n}}\max _{1\le k\le n} \left| \sum _{t=1}^{k} (\hat{\varvec{\phi }}^T \hat{\varvec{\epsilon }}_{t-1})^2 \right. \\ &\qquad -\left. \frac{k}{n}\sum _{t=1}^{n} (\hat{\varvec{\phi }}^T \hat{\varvec{\epsilon }}_{t-1})^2 \right| + \frac{2}{\sqrt{n}}\max _{1\le k\le n} \left| \sum _{t=1}^{k} {\hat{\epsilon }}_t \hat{\varvec{\phi }}^T \hat{\varvec{\epsilon }}_{t-1} - \frac{k}{n}\sum _{t=1}^{n} {\hat{\epsilon }}_t \hat{\varvec{\phi }}^T \hat{\varvec{\epsilon }}_{t-1} \right| \\ &\quad {:}{=} I_n + II_n, \end{aligned}$$

wherein

$$\begin{aligned} I_n \le&\frac{2}{n} \left( n \| \hat{\varvec{\phi }} \|^2 \right) \left( \frac{1}{n} \sum _{t=1}^{n} \| \hat{\varvec{\epsilon }}_{t-1}\|^2 \right) =o_P (1) \end{aligned}$$

because ${\hat{\sigma }}_t^2\ge 1$ for all t and

$$\begin{aligned} \frac{1}{n} \sum _{t=1}^{n} \|\hat{\varvec{\epsilon }}_{t-1}\|^2 \le \frac{1}{n} \sum _{j=1}^{p} \sum _{t=1}^{n} \sigma _{t-j}^2\epsilon _{t-j}^2 =O_P (1). \end{aligned}$$

To deal with $II_n$, we write $II_n \le 2\sqrt{n}\|\hat{\varvec{\phi }}\| (II_{n,1} + II_{n,2})$ with

$$\begin{aligned} II_{n,1}= & {} \frac{1}{n}\max _{1\le k\le n} \sum _{j=1}^{p} \left| \sum _{t=1}^{k} \left( {\hat{\epsilon }}_t {\hat{\epsilon }}_{t-j} - \epsilon _t \epsilon _{t-j} \right) - \frac{k}{n} \sum _{t=1}^{n} \left( {\hat{\epsilon }}_t {\hat{\epsilon }}_{t-j} - \epsilon _t \epsilon _{t-j} \right) \right| ,\\ II_{n,2}= & {} \frac{1}{n}\max _{1\le k\le n}\sum _{j=1}^{p} \left| \sum _{t=1}^{k} \epsilon _t \epsilon _{t-j} - \frac{k}{n} \sum _{t=1}^{n} \epsilon _t \epsilon _{t-j} \right| . \end{aligned}$$

Note that

$$\begin{aligned}&|{\hat{\epsilon }}_t{\hat{\epsilon }}_{t-j}-\epsilon _t \epsilon _{t-j}|\nonumber \\&\quad \le |{\hat{\sigma }}_t{\hat{\sigma }}_{t-j}-\sigma _t\sigma _{t-j}| |\epsilon _t\epsilon _{t-j}|\nonumber \\&\quad \le \Big \{ |{\hat{\sigma }}_t^2 -\sigma _t^2|\sigma _{t-j} +|{\hat{\sigma }}_t^2 -\sigma _t^2\|{\hat{\sigma }}_{t-j}^2 -\sigma _{t-j}^2|+ \sigma _t |{\hat{\sigma }}_{t-j}^2 -\sigma _{t-j}^2|\Big \}|\epsilon _t\epsilon _{t-j}|/2. \end{aligned}$$

(12)

Moreover, as

$$\begin{aligned}&\sigma _t^2= \frac{1}{1-\beta } +\sum _{j=0}^\infty \alpha \beta ^j y_{t-1-j}^2,\\&{\hat{\sigma }}_t^2= \frac{1-{\hat{\beta }}^t}{1-{\hat{\beta }}}+{\hat{\beta }}^t y_0^2 +\sum _{j=0}^{t-1} {\hat{\alpha }}{\hat{\beta }}^j y_{t-1-j}^2, \end{aligned}$$

on the event $( |{\hat{\alpha }} - \alpha | \le \rho , |{\hat{\beta }} - \beta | \le \rho )$ with $\rho <1$, whose probability tends to 1, for any $N \ge 1$, we have

$$\begin{aligned} {\hat{\sigma }}_t^2 - \sigma _t^2= & {} \frac{1-{\hat{\beta }}^t}{1-{\hat{\beta }}}+{\hat{\beta }}^t y_0^2 - (1-\beta )^{-1} + \sum _{j=0}^{N} ( {\hat{\alpha }} {\hat{\beta }}^j - \alpha \beta ^j ) y_{t-1-j}^2 \nonumber \\&+ O\left( \sum _{j=N+1}^{\infty } \lambda ^j y_{t-1-j}^2\right) \end{aligned}$$

(13)

for some $\lambda \in (0,1)$. Combining (12) and (13), we can easily show that $II_{n,1}\le \frac{2}{n}\sum _{j=1}^{p} \sum _{t=1}^{n} |{\hat{\epsilon }}_t {\hat{\epsilon }}_{t-j}-\epsilon _t \epsilon _{t-j}| =o_P(1)$. Then, since $II_{n,2}=O_P (1/\sqrt{n})$ by Donsker’s invariance principle for martingales (Billingsley, 1968), we have $II_n = o_P (1)$. This completes the proof of (5).

Moreover, using (13), the invariance principle, and the fact that

$$\begin{aligned} {\hat{\epsilon }}_t^2 -\epsilon _t^2= \frac{(\sigma _t^2-{\hat{\sigma }}_t^2)^2}{\sigma _t^2{\hat{\sigma }}_t^2}\epsilon _t^2 + (\sigma _t^2-{\hat{\sigma }}_t^2)\frac{\epsilon _t^2}{\sigma _t^2}, \end{aligned}$$

we can see that

$$\begin{aligned} \frac{1}{\sqrt{n}}\max _{1\le k\le n}\left| \sum _{t=1}^k {\hat{\epsilon }}_t^2-\frac{k}{n}\sum _{t=1}^n {\hat{\epsilon }}_t^2 -\sum _{t=1}^k\epsilon _t^2+\frac{k}{n}\sum _{t=1}^n \epsilon _t^2\right| =o_P (1) \end{aligned}$$

(14)

(see also Oh & Lee, 2018), which entails ${\hat{T}}_{n,2}-T_{n,2}=o_P (1)$ and the weak convergence of ${\hat{T}}_{n,2}$ to the supremum of the Brownian bridge. This validates the theorem. $\square$